0.2.0 - Polynomial Regression
Different datasets have different underlying structures, while some have linear underlying structures other can have nonlinear structures:
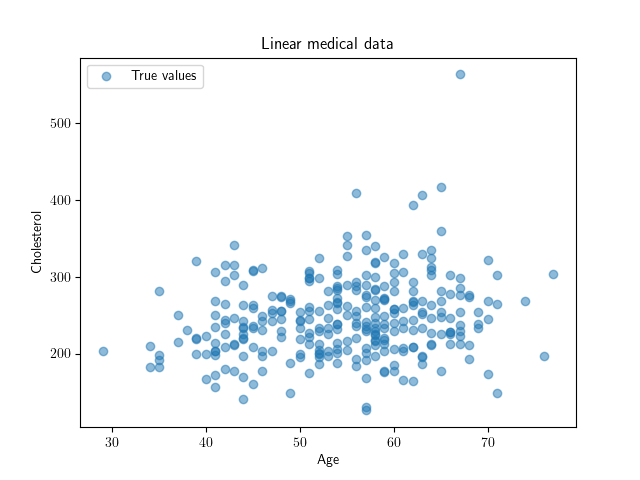
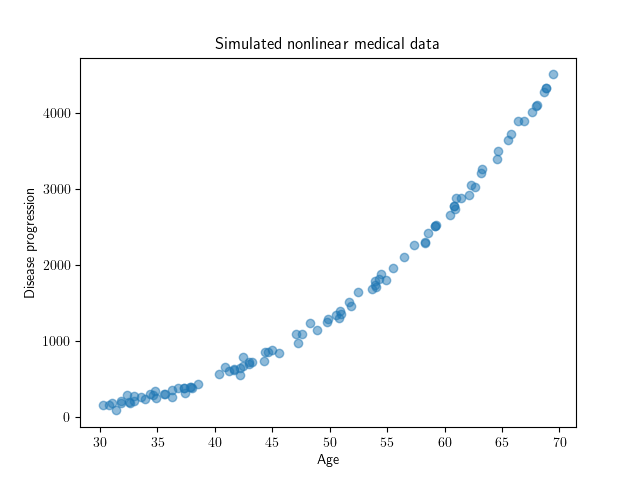
The differences are notable. When applying linear regression to both cases, it is apparent that linear regression is not a good way to model the nonlinear dataset.
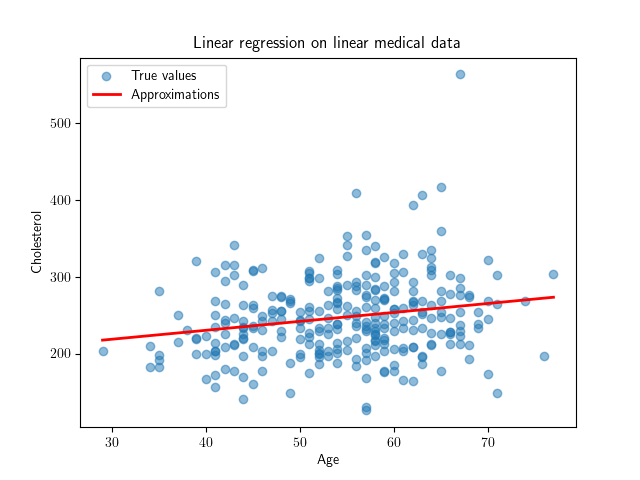
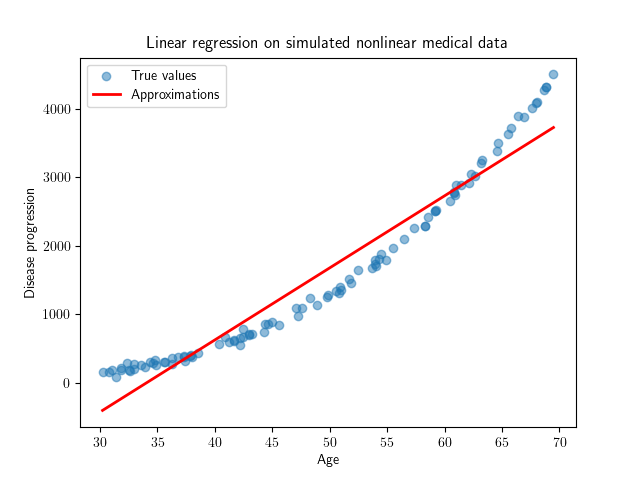
To capture the non-linearity better we utilize the fact that, in theory, a polynomial can approximate any continuous function over a closed interval (the Weierstrass Approximation Theorem). We know from linear regression that the linear model that predicts y is at the form:
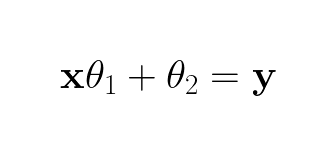
This a polynomial of 1. degree, which is a linear function. To achieve a non-linear function it has to be of, at least, 2. degree. There are two ways we could make the equation to be of 2. degree. Firstly we could make it non-linear with respect to the thetas by adding an extra term of 2. degree:
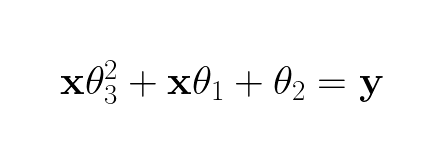
However, since we do linear regression so the model needs to be linear with respect to the θs/weights, the y has to be a linear combination of the columns, therefore this is not viable option. The other option we could do is to make the x of the added term a variable of 2. degree:
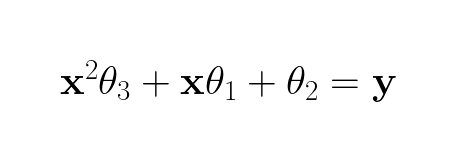
With respect to x this function is non-linear, while with respect to the weights the function is linear, which is exactly what we want!
This is a neat way to encode non-linearity into linear regression. To find the weights for this equation one only needs to fill in the normal equation:
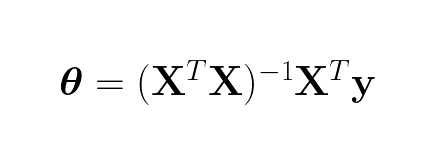
Using these weights we can find a model that fits much better than the linear model:
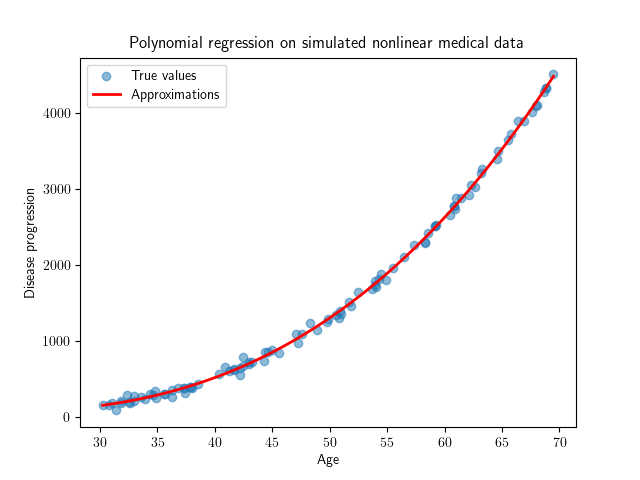
The choice of including a squared x term as input to the model is a form of feature engineering. We transform the the input x to be x² and add it to the model, making the model fit the underlying structures of the data better.
There are some trade-offs using polynomial regression, the most characteristic is that it can capture complexity but are more prone to overfitting. When you overfit you include all the noise into your model which hurts the accuracy of the model in real world scenarios. In addition to these tradeoffs, the same trade-offs that are true for linear regression are also true for polynomial regression.